
本篇文章来源冰衡活跃图纸交流群群友Benson Yang,也欢迎大家踊跃投稿!
人生要有目标,做事要有目的。我们计算过程能力是为了什么目的?

这事还要从两者的公式来说。观察下面公式,可发现一个共同之处:
1.分母都是σ 2.分子都是SPEC 3. 考虑位置,Ppk& Cpk还有均值
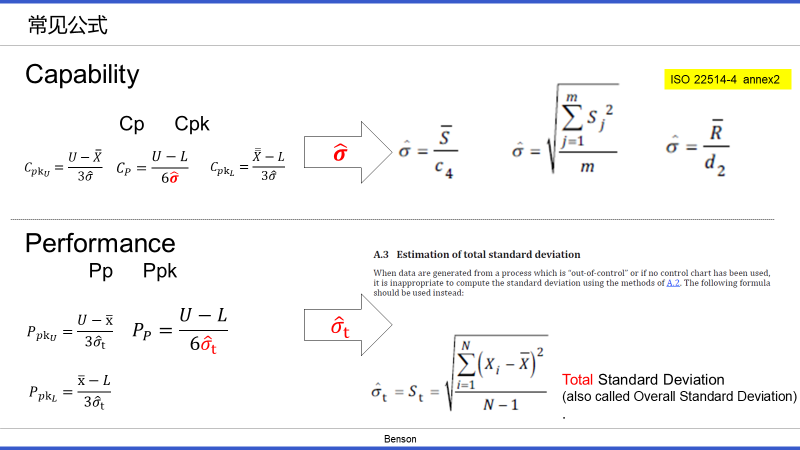
“规格在上,6σ在下“到底比较什么?
让我们来看下标准是怎么解释的。

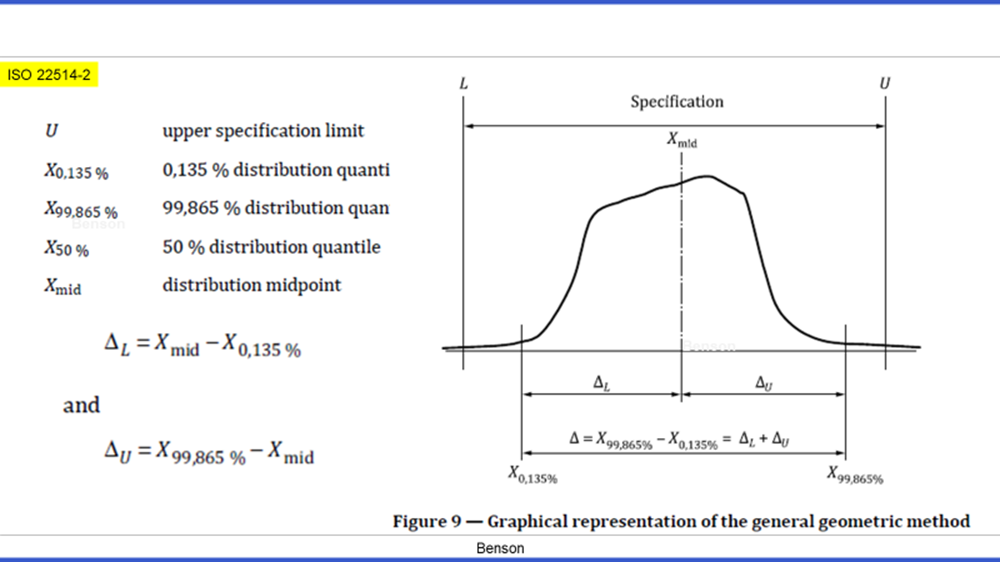
压根没有6σ!!!!

卷2的分母变为了 Δ ,描述了0.135%-99.865%的数据分布。换而言之整个数据的99.73%。Δ 由 中位数(midpoint/X50%)分割。
基于卷二的定义;当我们计算Cp/Pp 时,是为了比较 Δ(99.73%数据分布) 和 规格范围 考虑位置计算Cpk/Ppk 时,是为了比较 明确 分布中心位置(X50%/midpoint) 在SPEC中的位置。


中位数+99.73% vs 均值+6σ , 不矛盾嘛?
正态分布时不矛盾
“正态分布”在生活中经常出现,如人的身高;机器制造的产品的大小;测量误差;血压;考试分数。又如高尔顿钉板。虽然初衷是为了验证二项分布,但是最后却成了正态分布。
(每个钉都是一个二项分布,不是向左就是向右。所以二项分布的极限接近于正态分布)
事物由很多原因造成的且没有一个主要原因,就会形成正态分布。

“ps:虽然正态分布又叫高斯发明是为了纪念高斯。高斯“只是”站在巨人的肩膀上,推导出了其函数。”

当数据呈现正态分布时,会有以下特征:
1、均值左右3个σ,覆盖了分布的99.73%。
2、均值=中位数=众数;
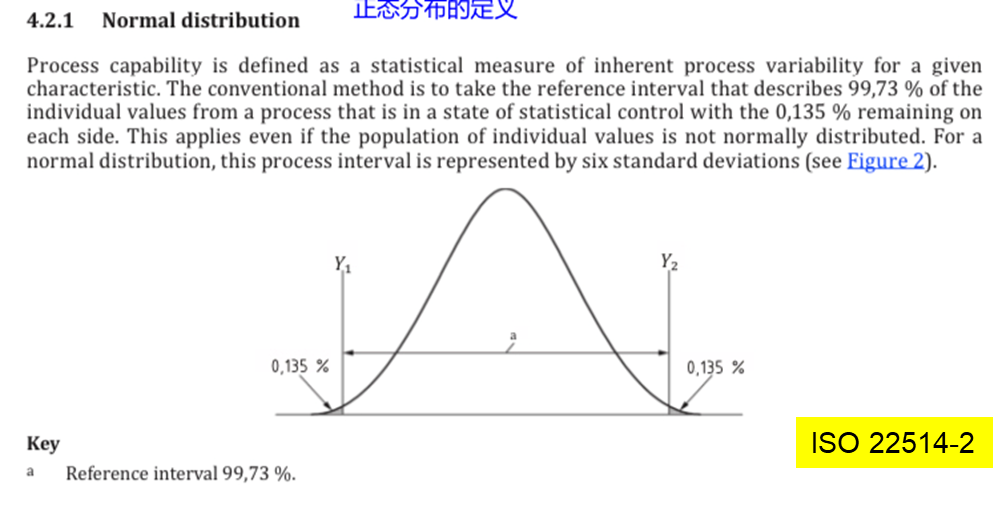
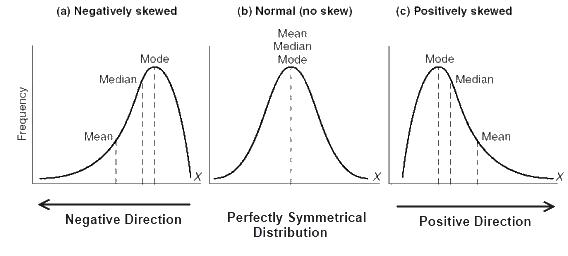
检验正态分布时,往往需要考虑分布的偏度和峰度。
当数据不服从正态分布时。例如偏态分布时,正态分布均值≠中位数≠众数。99.73%的数据并不集中在均值附近。

所以我们常见公式(带有σ和均值)只能用于正态分布的情况
但是实际生活中数据的分布有很多,也并不全部服从正态分布。
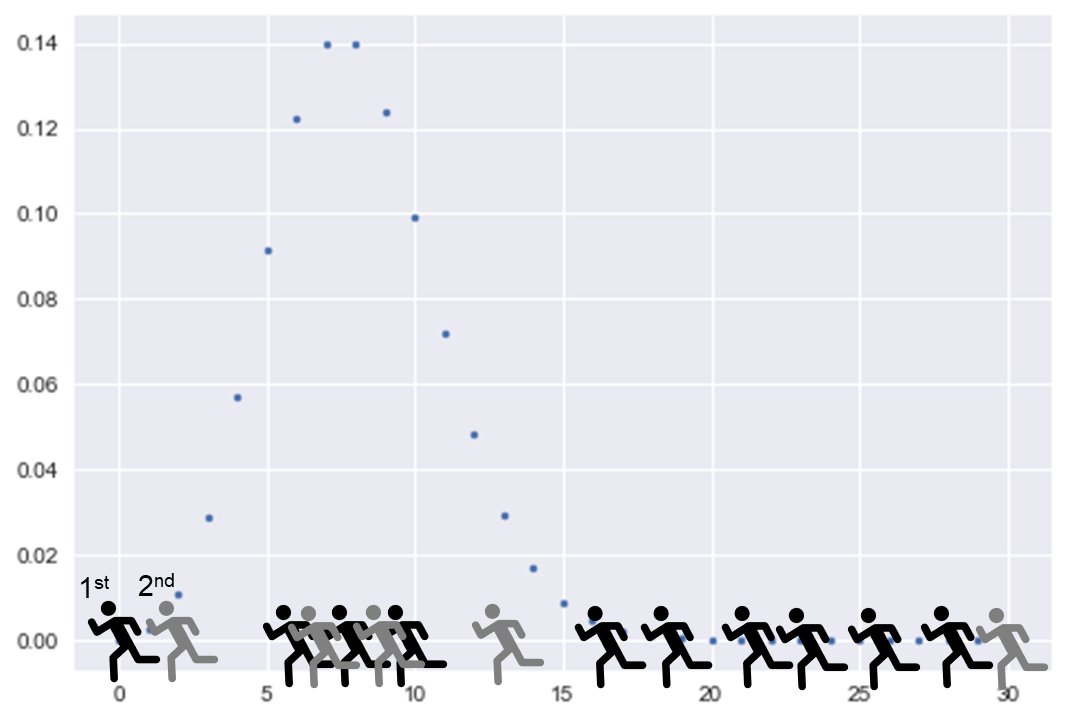
拿田径比赛为例,运动员的跑步成绩可能更加倾向于偏态分布甚至是泊松分布。比赛中,往往大部分人集中行程第二梯队,第一和第二名形成第一梯队,第三梯队由相互之间差距较大的一群人组成。
让我们重新回到ISO 22514-2。表4,表3 列举了各种方法


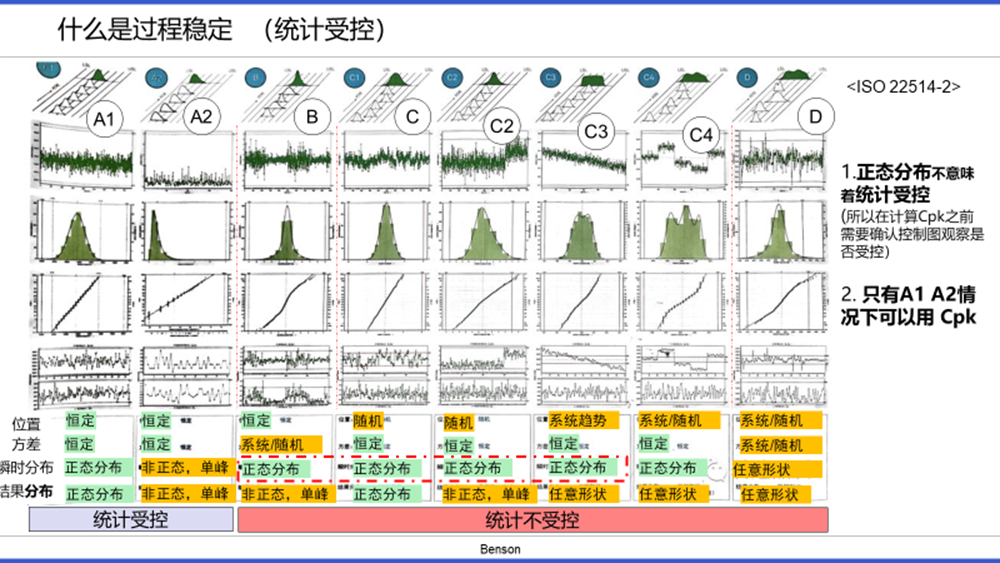
当数据呈现非正态分布(卷二除了 A 和 C1 以外的情况),描述位置使用2&4方法(中位数),分布(dispersion)使用1&5方法。*卷二中B不是正态分布,却可以用σ来评价。(表示不理解) 关于d1怎么操作。卷二 6.1.4 给出了 具体的操作方法。


说白了 按大小排列数数。
所需要的样本量巨头,至少1000的样本。

1000 个样本对于质量管控来说的代价是巨大的。虽然随着各种软件的出现,计算再也不是难事。
对于零件,获得1000个数据意味着耗费大量得实验测量资源。
所以无论是日常操作还是6σ的教材中,遇到非正态分布时,往往推荐转化正态分布的方法。
为何不在计算能力前,先看一下数据分布呢。
真正科学的质量管理在于 花 可能少的代价 管 好质量。
最后, 总结一下:
1、统计受控 ≠ 正态分布
2、统计不受控时不能计算Cpk & Cp
3、非正态分布不能使用 均值 和 σ ,使用前需先进行转化。
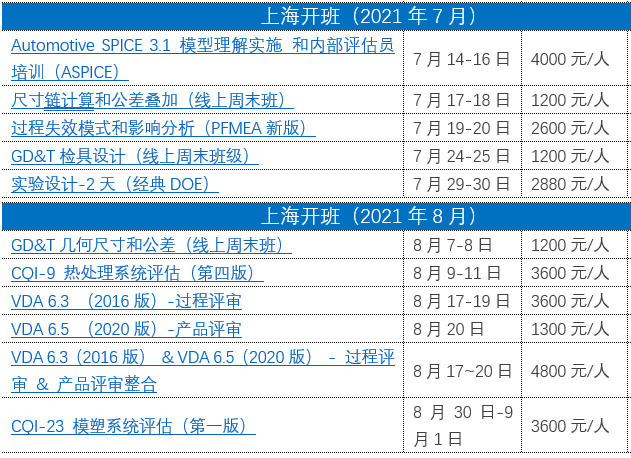
近期课表:
总有一群老法师,执着于最前沿的研发和质量领域,为中国制造业增强竞争力
专注研发流程优化和质量改善 - 冰衡中国

他们是:
研发流程专家
GD&T专家
CQI专家
创新设计思维专家
质量专家
...
他们是业界资深而低调的实战专家




