前言
在GD&T图纸中,最大实体M圈标注尤其很多,标注最大实体后,相应的公差就会得到补偿(放大),也就是这时公差不是一个固定值,是随着孔的大小改变而改变的。公差不固定,那么在做过程统计时,CPK怎么计算?这个问题一致是工程师头疼的问题。
前段时间公众号发表了一篇关于MMC的CPK计算问题,很多读者反应是英文版,不方便阅读。在广大读者的要求下,本公众号特此发表了由上汽集团资深专家翻译的中文版。
最大实体要求下的过程能力指数计算方法
目标:
描述一种位置度能力指数的计算方法。对于适用该位置度的每个零件,其公差各不相同。
范围:
适用于须确定零件图样中最大实体状态下位置度标注的能力指数的情况。本文并不讨论除Cpk计算以外的统计方法及“正态性”。关于更深入的统计方法参考资料,可在很多统计参考书籍与文献中查找得到。另外,读者应熟悉几何尺寸与公差标注。
定义:
MMC — 最大实体状态 — 表示零件要素处于实体最大的状态。在图样中以M标注。
LMC — 最小实体状态 — 表示零件要素处于实体最小的状态。是与MMC相反的一种状态。用GDT符号L来标注。
对于圆环,其最大实体状态指的是当其圆孔尺寸最小的时候。其最小实体状态则正好相反。
位置度— 尺寸要素的期望位置 — 及该位置允许的波动量。用GDT符号来标注。
补偿公差— 当要素偏离其最大实体(实体最大)状态时,所允许的额外公差值。
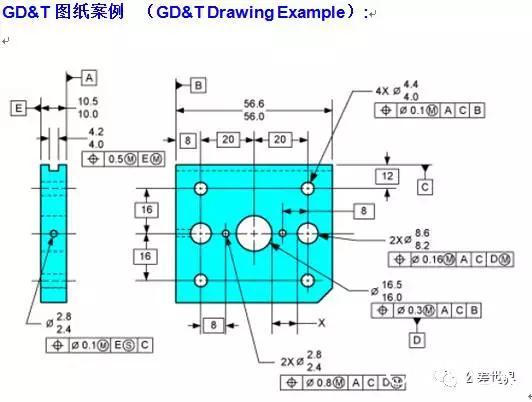
为了示范,使用如下的零件图样示例。处于本文的目的,我们假设该位置很“关键”,即需要确定过程能力。为了简化分析,只使用了5个样件。
在上面的平面视图中,外径(OD)是基准A。当内径(ID)处于其最大实体状态且OD也处于其最大实体状态时,ID相对于基准A(OD)允许的位置度波动量或位置范围是0.05。OD的尺寸公差带总共是0.2,ID也一样。
该零件的最大实体状态(使用圆环的算法)是ID 3.9,OD 5.1,此时ID允许的最大位置偏差是0.05。
测量了5个零件,结果如下:
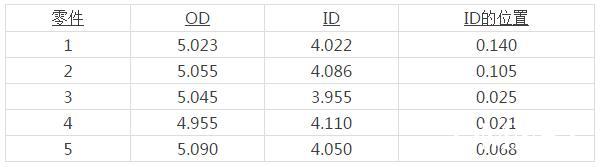
乍一看来,1号、2号、4号、5号零件似乎有问题。实际上,4号零件(ID)是超差的,一般不会用来评估。不过,出于进一步说明的目的,将其保留。1号、2号、5号零件的位置度看起来是超差的,让我们来详看一下……
Cpk计算的步骤
需通过几个步骤来计算Cpk。第一步已完成,即测量零件。第二步是计算每个零件的上公差。为了得到此结果,须首先确定每个零件的补偿公差。
1. 计算补偿公差
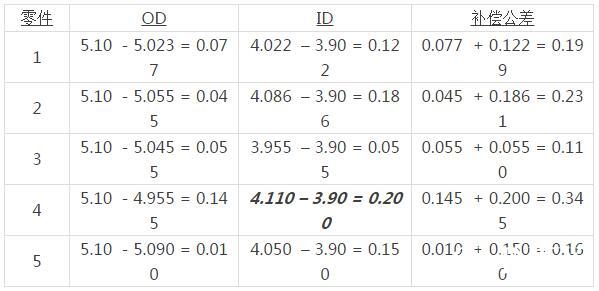
计算补偿公差时,首先要确定公差框格指向的每个零件要素的尺寸,然后计算这些尺寸与(最大)实体状态的差值。例如— 上面的1号零件:
5.10 – 5.023 = 0.077(最大实体状态减去实际尺寸)
4.022 – 3.90 = 0.122(实际尺寸减去最大实体状态)
2. 计算每个零件的上公差
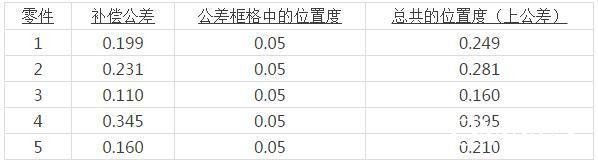
下一步,加上公差框格中规定的实际位置度值。在本例中是0.05。如果是0的话,则不用做这一步加法计算。
所以,对于1号零件,0.199 + 0.05 = 0.249。这就是1号的上公差。
注意到4号零件的补偿公差应该是0.355。然而该ID是超差的,所以不能将超过图样允许的补偿计算在内。(是的,这个零件实际上应当拒收,但为了进一步的说明而将其保留。如上所示,被测ID是4.110,而公差上限是4.10。)
3. 计算公差使用率
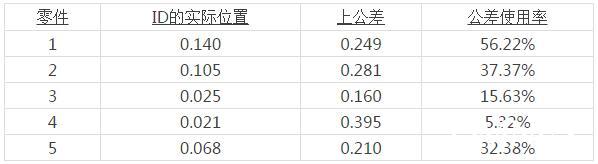
下一步,将ID的实测位置与允许的(即总共的)位置度进行比较。计算相应上公差的实际使用率。(见第5页的数值)
例:1号零件 0.140/0.249 = 0.5622或56.22%
4. Cpk计算
既然有了每个零件公差使用率的确定方式,我们就有了共同的上公差— 100%,及允许公差的100%。为了让统计软件计算,要用小数形式来表达,和百分比效果相同。
本例中(包括4号零件):
平均值 29.38%(或0.2938)
标准差 0.197591
Cpk是
上公差是1.00(或100%)
Cpk = = = 1.19
Cp是
上公差是1.00(或100%)
Cp = = = 1.69
附录
下表是计算表格展开的示例,包含了以上的所有数据。最后一列是分析的数据。我的统计软件经验是使用展开表来输入相应的数据,然后是公式,这样比人工计算方便得多。然后输入公差使用率。数据输入完毕后,我将这一列导入到软件包中区。
本例中,小数的表达方式是百分比。当导入到数据包里去时,这些数值需用小数的形式来表示。
平均值和其他计算也仅做展示用。其实可以依靠统计包来完成。对于MMC或LMC,上公差始终是1(1.00或100%)。





