今天这篇文章我们来探讨一下动态轮廓度和复合轮廓度之间的异同。
本篇文章将分3个部分来探讨:
1. 平移和偏置
2. 平面的复合轮廓度和动态轮廓度
3. 曲面的复合轮廓度和动态轮廓度
一. 平移和偏置
在探讨之前,我们首先来认识两个重要的动词,“平移”(Translate)”和“偏置(Offset)”。
平移,就是将特征上所有的点平行移动形成新的特征。相当于我们大学力学概念里的平动(还有一个不同的运动是转动),其中移动的过程中不能旋转。假设我们把一个圆弧往上平移2毫米,具体见下图。
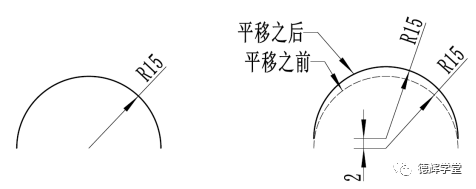
图1 平移
从图1中我们可以看出,平移后的曲线和原来的曲线形状大小一样,曲率半径没有发生变化,但是圆心的位置发生了变化(2毫米)。
偏置,就是将特征上所有的点向法向方向移动一定距离后形成新的特征。很多3D软件里有一个命令“Offset”,指的就是这个偏置操作。假设,我们把同样一个圆弧往外偏置2毫米,具体见下图:
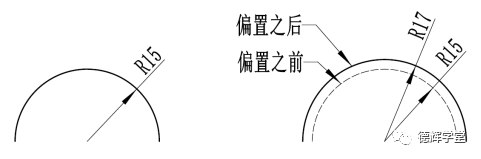
图2 偏置
图2就是将同样的圆弧偏置后形成的新的圆弧。我们可以看出其特点,如果将半径为15的圆弧“往外”偏置2毫米后,该圆弧的曲率半径变化了,由原来的R15变成偏置之后的R17,但是圆心的位置没有变化,也就是说偏置有“放大”或者“缩小”特征的能力。
大家如果仔细比较一下图1中的平移和图2中的偏置这两个动作,我们会发现2个特点:
1. 平移不会改变曲率半径,但会改变圆心位置;偏置会改变曲率半径,但不会改变圆心位置。
2. 偏置尽管会改变曲率半径,但是经过偏置改变曲率半径后的新圆弧和偏置之前的圆弧的视觉“相似度”很高(观察图2)。而平移前和平移后的视觉相似度却不高(观察图1)。
有关平移和偏置的这个特点,我们把它称为平移偏置常理1。
当然,也有一种情况,平移和偏置没有区别,那就是当平移和偏置的对象是直线或者平面时,具体见下图:
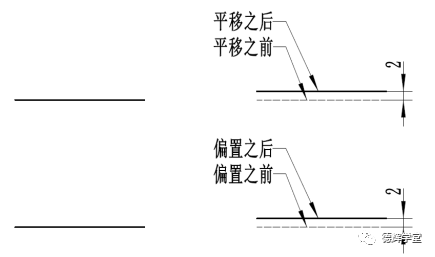
图3 平移和偏置
显然,从图3可以看出,对直线或者平面进行偏置或者平移后,两者没有任何区别。这是因为直线或者平面的曲率半径为无穷大。平移本身不能改变曲率半径,而偏置也不能改变曲率半径。
当对平面或者直线进行平移和偏置处理时,两者没有任何区别。这种现象我们在本篇文章里把它称为平移偏置常理2。
我们为什么要讨论平移和偏置这两个貌似无聊的动词呢?因为轮廓度公差带的边界就是由这两个动作形成的。理解了这两个动词的本质,我们就能够更加深入的理解复合轮廓度和动态轮廓度。
一. 平面的复合轮廓度和动态轮廓度
提起复合轮廓度,往往给人的感觉就是高大上,还可以用来装逼(那些趾高气扬的面试官就经常不怀好意地拿复合轮廓度来考核面试者)。今天我们好好认识一下高逼格的复合轮廓度。
复合轮廓度事ASME标准特有的术语,ISO和国标是没有的。它其实非常简单,就四个字“基准阉割”。它阉割的对象是复合轮廓度第二行和第二行以下的所有基准,让这些被阉割的基准只能约束公差带的方向,不能约束位置。
我们举个例子来认识基准是如何被阉割的。

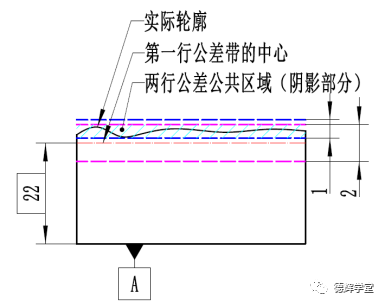
图4 复合轮廓度和公差带
图4中的轮廓度就是复合轮廓度。它有两行,且两行都共享一个轮廓度符号(凡是几行共享一个轮廓度符号的轮廓度都叫复合轮廓度)。
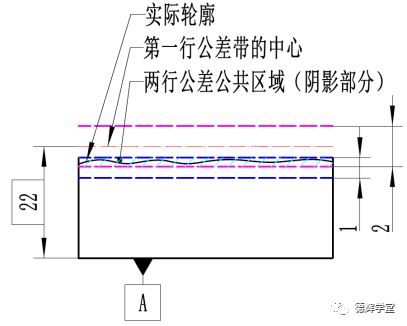
既然有两行,所以复合轮廓度中第一行和第二行都有自己的公差带,具体见图4中的下图。紫色的公差带是第一行的公差带。复合轮廓度第一行的公差带是正常的,它必须和基准A保持理想的方向和位置关系,即紫色的公差带必须要和A绝对平行,而且紫色公差带的中心必须和基准A保持绝对的22的距离。
复合轮廓度的关键在于分析第二行的公差带(图4中蓝色的公差带)。我们说了,第二行的基准A是被“阉割”过的(注意,定义就是这样的,它命不好),它只能约束蓝色公差带的方向,不能约束公差带的位置。即宽度为1的蓝色公差带只需要和A保持方向关系(绝对平行),不需要保持位置关系,也就是说,理论尺寸22对蓝色公差带没有意义,蓝色的公差带可以上下浮动。

A
B
C
图5 复合轮廓度公差带的变化趋势
见图5中的A,B,C图,第二行蓝色的公差带宽度为1,可以上下任意平移。被测特征要合格的话,必须满足以下两个条件:
1. 第一行紫色公差带和第二行蓝色公差带有交集(如图5 A,B,C中的阴影部分)
2. 被测要素(实际被测表面)必须落在交集以内
相信有很多小伙伴到这里感到不对啊,第二行蓝色的公差带可以上下浮动,它和平行度不是一样的吗?
没错,第二行确实是和平行度一样。

图6 复合轮廓度和平行度
这里的复合轮廓度第二行和平行度真的完全一样,因为他们的本质都是要求公差带必须要和基准保持理想的方向关系。
我们再来看看平面的动态轮廓。我们上一篇文章讲过了,动态轮廓度相当于偏置量为任意值的非对称轮廓度。
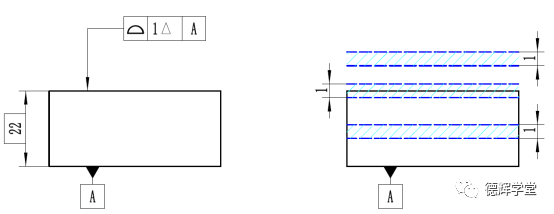
图7 动态轮廓度和公差带
图7中,因为动态轮廓度公差带宽度为1,且偏置量为任意值。所以公差可以上下任意偏置,根据平移偏置常理2,它其实和平移是一样的效果。所以图7中的动态轮廓度也相当于平行度,它也和复合轮廓度第二行的要求是一样的。
所以在本案例里边,复合轮廓度和动态轮廓度表达的对零件的要求是一样的。
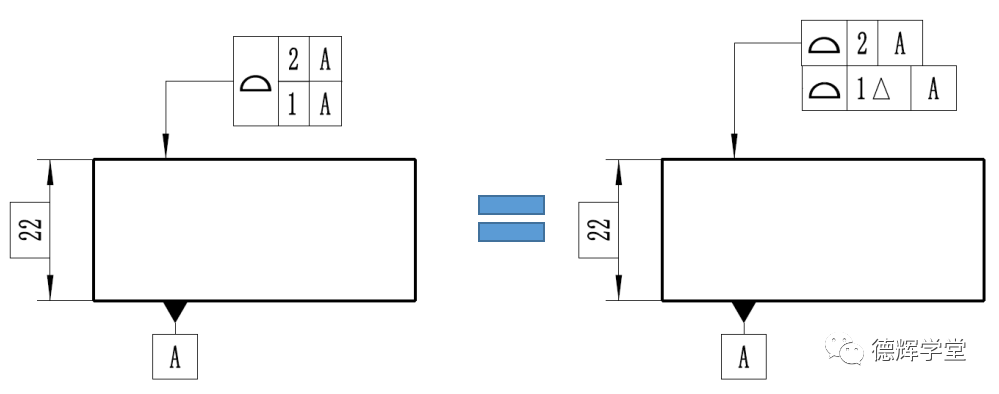
图8 复合轮廓度和动态轮廓度
图8表达了复合轮廓度等同于动态轮廓度的一个特殊的案例。这个案例说明复合轮廓度和动态轮廓度也有等同的时候,那就是因为平移偏置常理2。
注意,复合轮廓度和动态轮廓度等同的前提是被测面是平的。
而绝大部分情况下,复合轮廓度和动态轮廓度是不等同的。当被测表面是曲面(真正弯的那种曲面)的时候。
一. 曲面的复合轮廓度和动态轮廓度
1. 曲面的复合轮廓度
我们在知道平面的复合轮廓度公差带的特点后, 基于同样的原理,再来理解曲面的复合轮廓度就没那么困难了。直接上图:

A. 图纸标注
 B. 复合轮廓度公差带
B. 复合轮廓度公差带
图9 曲面复合轮廓度
同样的逻辑,第一行公差带是由两段半径分别为R41和R39的紫色圆弧组成,这个紫色的圆弧是由理论轮廓(半径为R40)内外各偏置1形成的。基于轮廓度的定义,这个紫色的公差带必须要和基准系ABC保持理想的方向和位置关系,显然,这时该公差带的六个自由度全部被基准系ABC锁死。
而图9中复合轮廓度第二行的公差带,它的两个边界半径分别为R40.5和R39.5(蓝色圆弧),这两个蓝色边界是由半径为R40的理论轮廓内外各偏置0.5形成,具体见图9中的B图。
又因为在复合轮廓度中,该第二行所有基准被阉割(即基准仅具备定向而无定位作用), 所以蓝色公差带只需要和A,B,C保持方向关系,公差带和A绝对垂直,和B,C保持与数模一样的方向关系,不需要保持位置关系。
也就是说第二行蓝色的公差带可以上下左右任意平移,但不能旋转。 最终,被测曲面要合格,同样满足下面两个条件:
1. 第一行紫色公差带和第二行蓝色公差带有交集
2. 被测要素(实际被测表面)必须落在交集以内
多说无益,具体看以下图例:
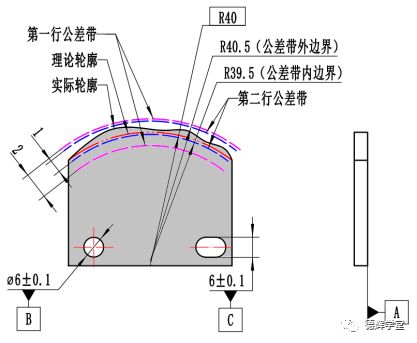
图10 第二行公差带(蓝色)可以往上移
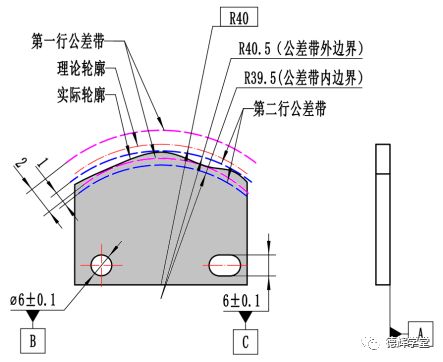
图11 第二行公差带(蓝色)可以往下移
需要注意的是,图11中,蓝色的公差带是可以超出紫色公差带的(再强调一遍,是公差带可以超出,被测要素不能超出!),而只要实际轮廓(即被测要素)能够落在紫色公差带(第一行)和蓝色公差带(第二行)的交集里边,说明该实际轮廓就满足该复合轮廓度要求。

图12 不应该出现的公差带(蓝色)旋转
图12中,就是我们一再强调的,图9A中的复合轮廓度第二行的蓝色公差带,它必须和基准ABC保持理想方向关系,不能旋转,不能旋转! 图12中出现公差带的旋转是不允许的。
好了,到这里我们阐述了复合轮廓度公差带的特点,尤其是第二行(第一行和普通轮廓度一样,没啥特殊的),我们再稍微回顾一下重点:
1. 复合轮廓度每行(重点是第二行或以下)公差带的两个边界的半径是一定确定的,因为它们是由理论轮廓内外各偏置固定数值(半个公差带)后形成的。比如本案例中,复合轮廓度第二行蓝色公差带的两个边界的半径是R39.5和R40.5,它们是由理论轮廓R40内外各偏置0.5形成的。
2. 复合轮廓度第二行蓝色公差带的两个边界半径尽管一样,但是因为位置可以上下左右平移,那么这两个蓝色圆弧边界的圆心,可以和理论轮廓的圆心同心,但绝大多数时候他们是不同心的。见下图:

图 13 公差带边界圆心和理论轮廓不同心
复合轮廓度第二行及以下公差带的特点是,先偏置(形成公差带),再平移(基准阉割)。
为什么要无聊的在这里强调上面两个明显的特点呢?
因为上面两个特点正是和动态轮廓度本质上不一样的地方!接下来,我们再来看看动态轮廓度的特点。
2.曲面的动态轮廓度
在本公众号前面一篇文章《非对称轮廓度与动态轮廓度》中讨论了动态轮廓度公差带的形成,为了更好的理解动态轮廓度,我们仔细来讨论一下它公差带的特点:

图 14 动态轮廓度
图14中采用了轮廓度加动态轮廓度来控制被测零件的曲面。本节专门讨论第二行的动态轮廓度公差带。它的公差带如下图:
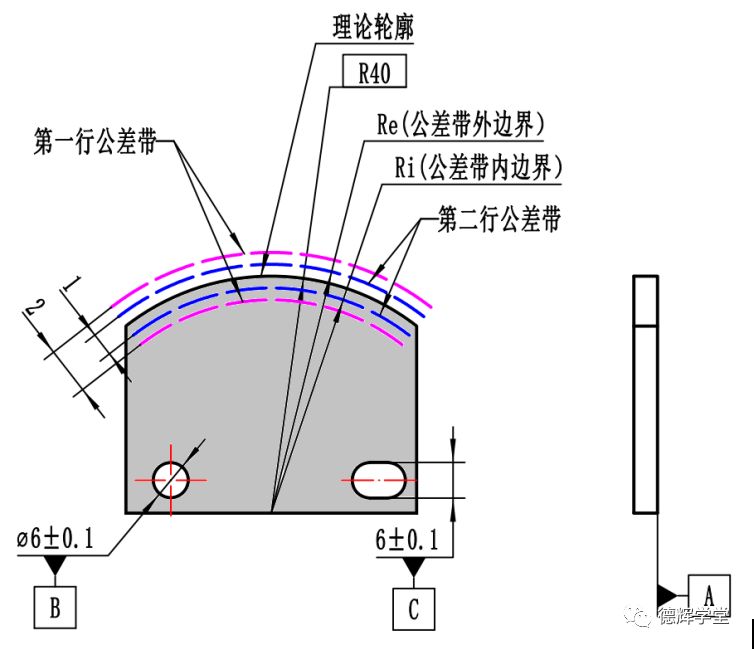
15 动态轮廓度公差带
图15中,动态轮廓度公差带, 是由两段半径分别为Re和Ri的蓝色圆弧组成,这两个蓝色圆弧是由理论轮廓偏置而来。
动态轮廓度的奇葩之处在于:
1. 公差带是由理论轮廓偏置而来,但是偏置量可以为任意值!即公差带的两个蓝色边界的半径大小(Re和Ri)不像复合轮廓度那样是固定值, 两个半径Re和Ri可以为任意值
2. Re和Ri之差必须是1(公差带宽度),即Re - Ri = 1
基于图14,我们再来看动态轮廓度公差带几个可能的情形:
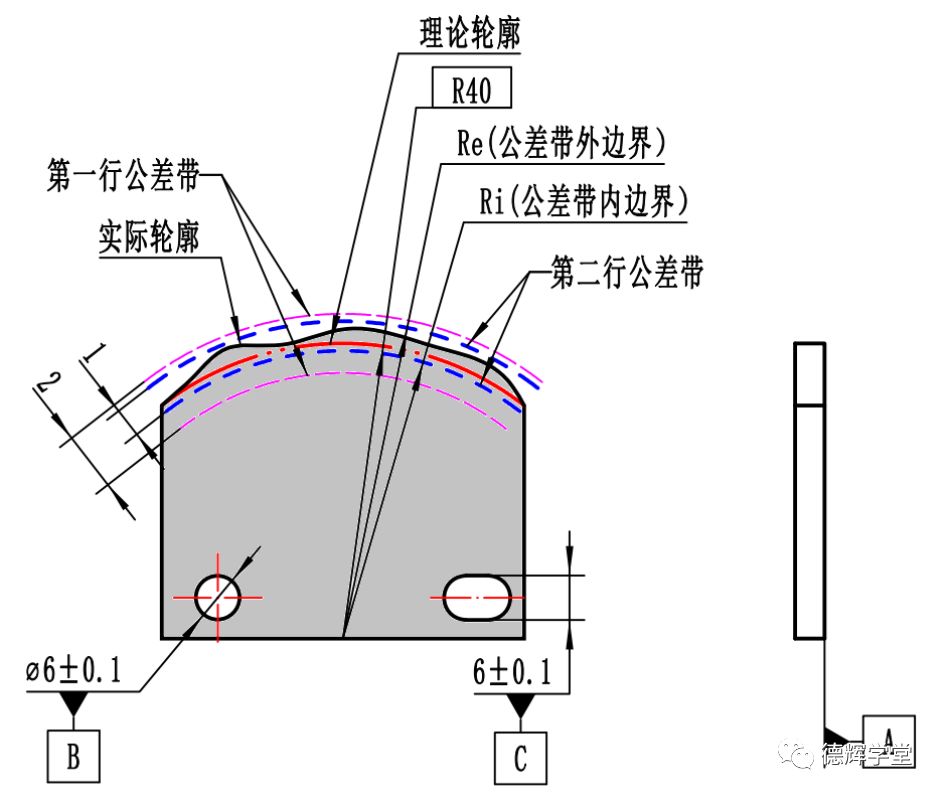
图 16 动态轮廓度公差带(一)

图 17 动态轮廓度公差带(二)
如果我们仔细观察动态轮廓度,再和复合轮廓度作比较,我们会发现,它的轮廓度貌似和复合轮廓度一样,可以上下“动”。但是动的特点不一样,
复合轮廓度的移动,它是因为公差带(第二行及以下)的位置不受任何基准的约束,所以公差带可以动,这个“动”,站在运动的角度,这叫“平移”,公差带的平移,当然会导致公差带圆心的平移, 所以公差带圆心和理论轮廓的圆心是不重叠的。
而动态轮廓度的动,不是平移,是偏置,不定量的“偏置”,即是“放大”或者“缩小”的过程。不过因为是偏置的动作,所以动态轮廓度的公差带的圆心永远和理论轮廓的圆心同心。
两者特点具体见下图:
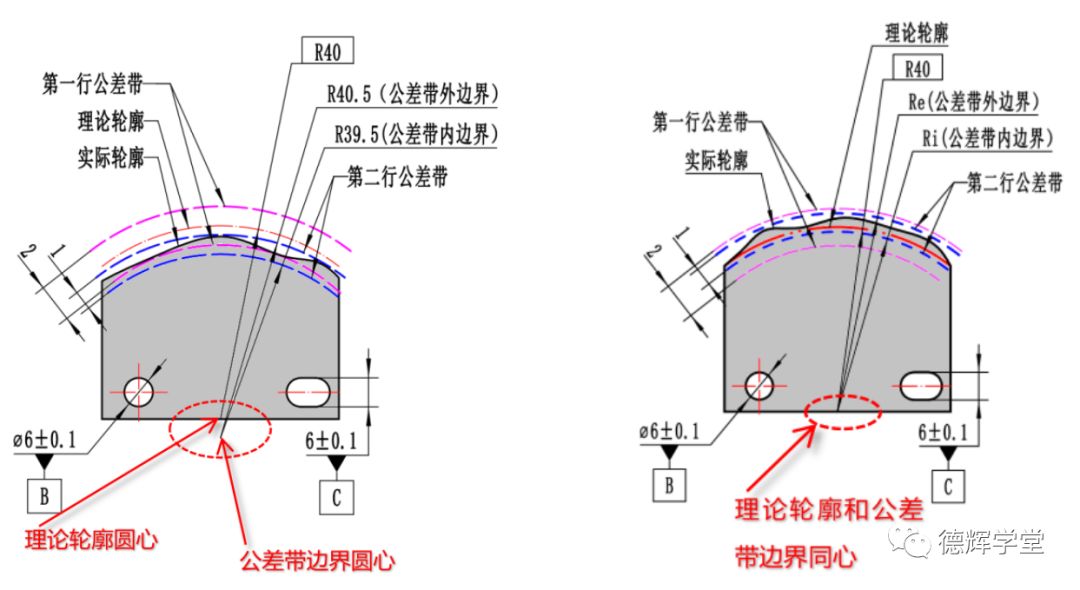
图18 复合轮廓度和动态轮廓度的差别
好了,到这里我们关于动态轮廓度的解释就暂时结束了。不过我们还是需要在这里重点强调的是:
复合轮廓度第二行及以下的公差带,它的公差带是由理论轮廓偏置形成的,偏置量是公差带大小的一半,但是偏置形成后的公差带是可以平移的,任意平移,直到能够把实际被测要素(被测表面)框进去为止。
而动态轮廓度的公差带,也是由理论轮廓偏置后形成的,偏置量可以为任意值,但它要求公差带两个边界偏置量之差为固定值,即为公差带的大小,只要形成的公差带能够把被测要素(被测表面)框进去就行。
本章小结
本篇文章分三个章节仔细探讨了复合轮廓度和动态轮廓度各自的特点。第一章节着重强掉“平移”和“偏置”两个不同的动作。第二章节则强调了对于平面来说,复合轮廓度和动态轮廓度是没有区别的,因为对平面来说,偏置和平移没有区别。第三节则强调被测要素是曲面时,复合轮廓度和动态轮廓度是有区别的,公差带各自的特点不一样,复合轮廓度的圆心相对于理论轮廓的圆心可以移动,而动态轮廓度的圆心相对于理论轮廓则不会移动。
讲到这里,可能有很多好奇的小伙伴会继续问,那动态轮廓度和复合轮廓度在设计应用上究竟有什么区别呢?如何检测呢?我们将在下一篇文章中继续讨论!




